This is a brief update on mix and match networks (M&MNets), describing the new ideas included in the extended version (IJCV 2020). An earlier post contains more details about the original CVPR 2018 version.
Mix and match networks (summary)
We are interested in the problem of cross-modal image-to-image translation between arbitrary pairs of modalities (here I will talk about modalities, but it can be applied to domains also). In particular, translations from modality \mathcal{X^{(i)}} to modality \mathcal{X^{(j)}} are implemented as the composition of a modality-specific encoder followed by a modality-specific decoder \mathcal{X^{(j)}}=g_j\left(f_i\left(\mathcal{X^{(i)}}\right)\right). The problem of zero-pair translation arises when we only have training for some of the translations (seen translations) while the rest need to be inferred (unseen translations).
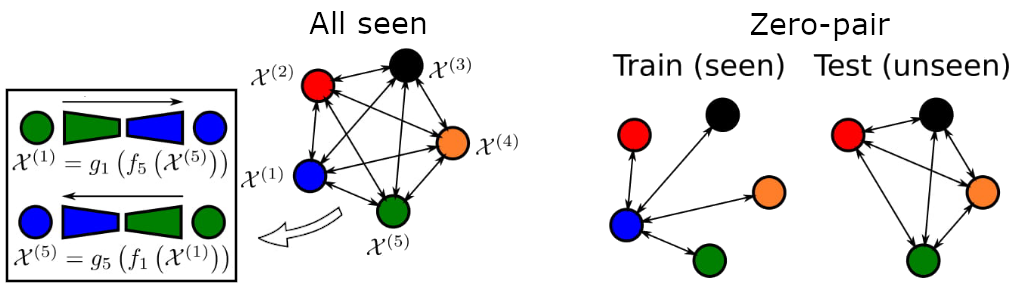
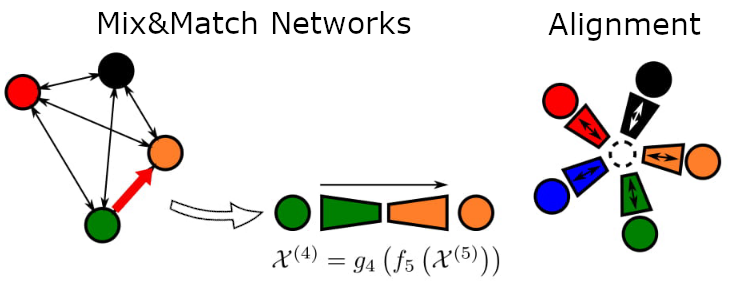
This requires that modality-specific encoders map to a common latent representation shared by all modalities. This requires a shared latent space containing the necessary information so any decoder can recover the image in the corresponding modality, even when those pairs of modalities haven’t haven’t been seen during training. M&MNets achieve that by enforcing alignment between encoders and decoders via modality-specific autoencoders, latent consistency losses, and using robust side information. For more detail, please read first the previous post.
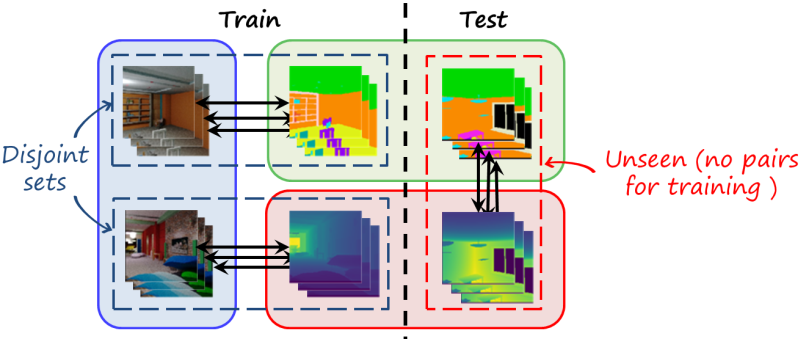
We focus on a particularly challenging cross-modal translation setting, where we have two seen training datasets, one with RGB images and their annotated segmentation maps, and another with RGB images (a different set) and the corresponding depth maps. Now the task is to infer segmentation from depth and depth from segmentation (i.e. unsee translations).
Shared and modality-specific information
M&MNets are able to obtain good results by using different tricks (latent space consistency, robust side information, autoencoders). However, we noticed that the original architecture (CVPR version) still didn’t fully exploit the shared information across modalities. The reason is that when we learn a particular translation, the modality-specific information is discarded (e.g. pure orange part in the segmentation modality), and the output image is recovered from the shared information across the two modalities. Since we only learn through seen translations, any shared information across modalities that is not useful for the seen translations will be discarded and not represented in the common latent representation.
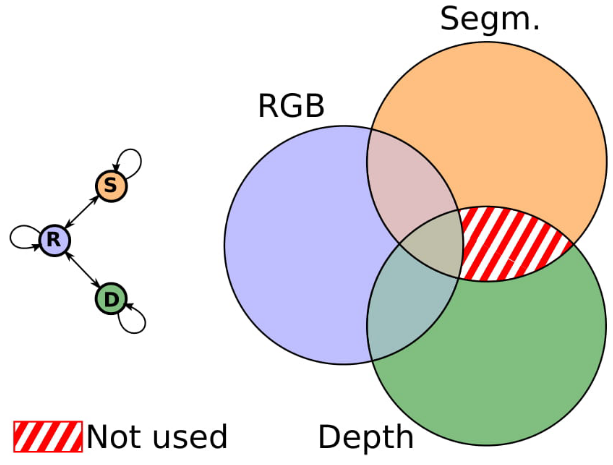
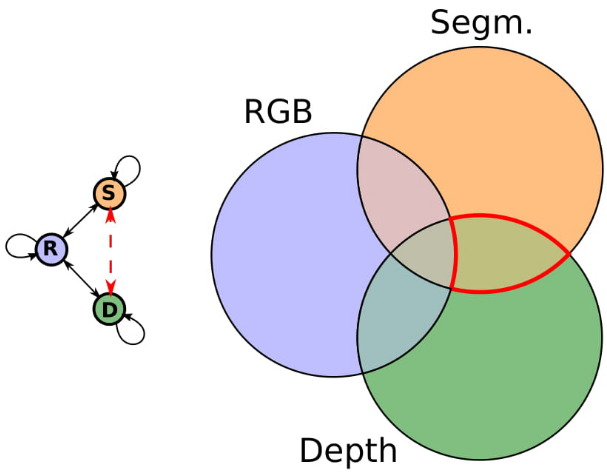
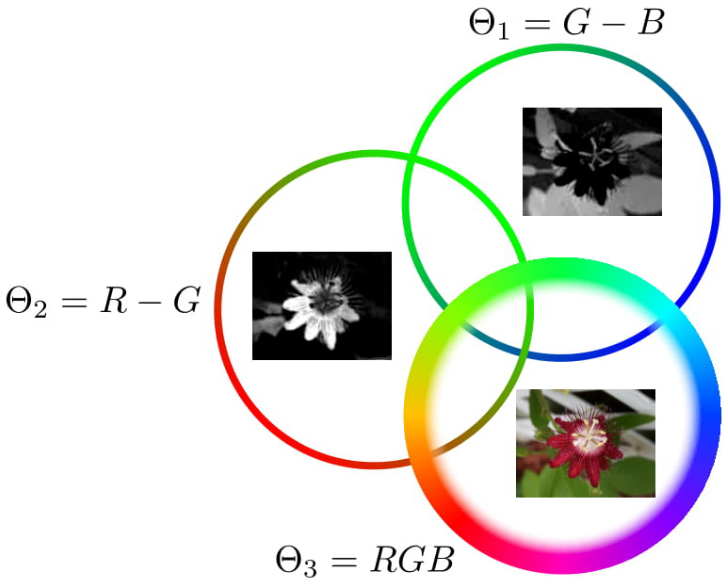
Thus, we would like to also exploit the unseen shared information and keep it in the latent representation. In our example, we want to keep shared information between segmentation and depth, even that that is not useful to recover the RGB image. This is tricky, since that cannot be achieved by simple seen translations. Below there is another illustrative example based on color opponents. We observe translations across color opponents \left(\Theta_1,\Theta_2\right) and from one color opponent to RGB \left(\Theta_1,\Theta_3\right), and we want to infer the translation from the other color opponent to RGB \left(\Theta_2,\Theta_3\right), which requires to complete the part of the color information that wasn’t seen.
Pseudo-pairs
In order to address this challenge, we take advantage of the idea of pseudolabels, used in unsupervised domain adaptation. Since we don’t have paired instances for unseen translations, we use predicted images from encoder-decoder combinations of seen translations, and create pseudo-pairs.
Using the cross-modal translation scenario to illustrate the idea, let’s recall that we have two datasets \mathcal{D}_{RS} and \mathcal{D}_{RD} with pairs of RGB and segmentation images \left(x^{(R)},x^{(S)}\right)\in \mathcal{D}_{RS} and pairs of RGB and depth images \left(x^{(R)},x^{(D)}\right)\in \mathcal{D}_{RD}. A translation T_{ij} from modality i to modality j is implemented as and encoder-decoder pair T_\mathcal{ij}\left(x^{(j)}\right)=g_j\left(f_i\left(x^{(i)}\right)\right).
Now we can leverage a training dataset \mathcal{D}_{RS} and the seen translator T_{RD} in the following way. We can use a pair \left(x^{(R)},\hat{x}^{(S)}\right)\in\mathcal{D}_{RS} and obtain a pseudo-depth image as \hat{x}^{(D)}=T_{RD}\left(x^{(R)}\right). Now we can create a pseudo-pair \left(x^{(S)},\hat{x}^{(D)}\right) and use it to train the unseen translator T_{SD}. Similarly we can create pseudo-pairs to train the reverse translation T_{DS}.
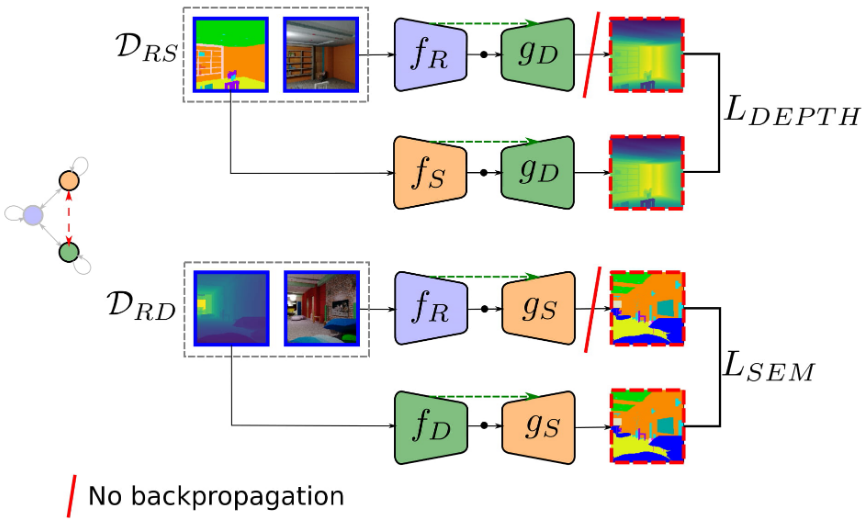
The previous figure shows the additional branches added to the original M&MNet framework for the cross-modal translation problem (see previous post for details) to exploit unseen shared-information. We also add a new loss term that enforces aligning the prediction using the corresponding error metrics for segmentation and depth
L_{PP} = \mathbb{E}_{(x^{(R)},x^{(S)})\sim \mathcal{D}_{RS}}\left[ \mathcal{B}\left(T_{RD}\left(x^{(R)}\right)-T_{SD}\left(x^{(S)}\right) \right) \right] + \mathbb{E}_{(x^{(R)},x^{(D)})\sim \mathcal{D}_{RD}}\left[ \mathcal{CE}\left(T_{RS}\left(x^{(R)}\right),T_{DS}\left(x^{(D)}\right)\right) \right]Finally, we observe that the segmentation and depth decoders T_{RS} and T_{RD} are already trained in parallel using the original training pairs. RGB-segmentation pairs are more reliable than pseudo-pairs segmentation (similarly for the other direction).
Examples
We first illustrate the importance of exploiting unseen information between domains with the color opponent scenario. In the following figure we can observe how the original M&MNets can’t recover certain color components and the resulting color is often different from the ground truth. In contrast, using cont. This also increased the recognizability of the resulting image, increasing from 36.5% a 57.5% (evaluated with a classifier trained on the original training images).

The next example illustrate how M&MNets can perform zero-pair cross-modal translation from depth to segmentation. Pseudo-pairs help to improve the zero-pair segmentation performance.

In conclusion, we revisited the mix and match networks framework. In this post we observe that the original framework didn’t exploit unseen shared information, which can be exploited using pseudo-pairs, further improving zero-pair translation.
References
Y. Wang, J. van de Weijer, L. Herranz, “Mix and match networks: encoder-decoder alignment for zero-pair image translation”, Proc. International Conference on Computer Vision and Pattern Recognition (CVPR18), Salt Lake City, Utah, USA, June 2018[supp][arxiv][slides][poster]
Y. Wang, L. Herranz, J. van de Weijer, “Mix and match networks: multi-domain alignment for unpaired image-to-image translation”, International Journal of Computer Vision, vol. 128, no. 12, pp. 2849–2872, Dec. 2020 [arxiv][link].
